コンテンツへスキップ
光ヘテロダイン干渉法を利用した複屈折測定
- 基本原理
複屈折性をもつ試料に,その主軸と偏光面とが一致するように2周波直交直線偏光(STZL発振光)を通過させることを考えます.それぞれの偏光成分が試料を通過する時の速度は,試料の「進相軸」方位と「遅相軸」方位とでは異なります.ですから,試料を透過した後では,「位相差」が生じることになります(複屈折・参照).従って,光ヘテロダイン干渉法を用いて位相差を検出することで,その試料のもつ複屈折量を高精度に定量測定することが出来ます.
複屈折測定の原理図を図に示します.直線偏光子は,2つの光を干渉させるために用いられています.この様な構成にすると,複屈折測定を電気位相計の測定精度で測定できます.電気位相計の測定精度は0.1度(以上)ですから,複屈折量を光の波長の4000分の1程度の高精度で測定できるわけです.
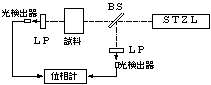
試料の屈折率をnx, ny光が透過する厚みをdとすると,透過後に生じる位相遅れ\(\phi _x, \phi _y\)はそれぞれ次のように表せます.
\begin{eqnarray}\phi _x = \frac{2n_x d}{\lambda} \tag{4} \\
\phi _y = \frac{2n_y d}{\lambda} \tag{5} \end{eqnarray}
STZL発振光を試料に透過させると,光検出器で得られる光強度信号Iは次のように表されます.
\begin{eqnarray}I &=& \langle|{E_x + E_y}|^2\rangle\\ &=& \frac{a_x^2+a_y^2}{2}+2a_x a_y cos\{2\pi (f_x – f_y)t + (\phi _x – \phi _y)\}\\ &=& \frac{a_x^2+a_y^2}{2}+2a_x a_y cos\{2\pi f_b t + \Delta\}\\ &=& \frac{a_x^2+a_y^2}{2}+2a_x a_y cos\{2\pi f_b t + \frac{2\pi (n_x – n_y)d}{\lambda}\}\\ &=& \frac{a_x^2+a_y^2}{2}+2a_x a_y cos\{2\pi (f_b t + \frac{\delta n d}{\lambda})\} \tag{6} \end{eqnarray}
ここで,\(\Delta\)は2成分光の位相差を,\(\delta n\)は屈折率差=複屈折量を表します.(6)式から,2つの光の位相差がビート信号の位相差に転化されていることが分かります.
以上のことから,光ビート信号の位相を電気位相計などで計測することで,複屈折量を測定できることが示されます.
- 主軸方位の同時測定
ところが,上の方法では,(1)試料の複屈折主軸の方位を予め求めて,(2)その主軸の方位をSTZLの発振偏光面に正確に一致させなければなりません.そこで,STZL発振光の偏光面を光軸の回りに回転させながら位相差の検出を行い,複屈折量とその主軸方位とを同時に求めます.
偏光面を光軸の回りに回転させるために,二分の一波長板の「入射偏光面と波長板の主軸とのなす角の2倍だけ出射偏光面を回転させる」という性質を利用します.
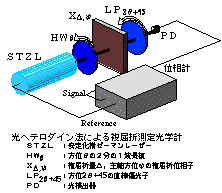
光ヘテロダイン法を用いて,複屈折量とその主軸方位とを同時に測定する光学系を,図に示します.この光ヘテロダイン干渉計において,STZL発振光の2つの偏光成分は,光源から光検出器まで,全く同一の光路を通ります.ですから,外乱—例えば振動や,空気揺らぎのような—による影響は,2つの偏光成分は全く同じだけ受けることになります.その結果,これらの外乱によるノイズ成分は全てキャンセルされてしまい,光ビート信号には全く影響を受けないことになります.
一般の光学的な干渉計は,振動とか空気揺らぎを取り除くような実験設備を必要としますが,この測定法によれば,そのような設備は必要ありません.このことは,光学的な測定をする上で大きなメリットとなります.
Back Main


