複屈折とは
- 光の屈折
空気中から,透明な材料に光が入射するとき,その境界で光は折れ曲がります.つまり,進行方向が変わるわけです.これは,空気と透明材料とでは性質が違うことが原因です.私たちの身近なところでは,お風呂とかプールに入ったとき自分の腕が水面のところで曲がって見えたり,水の中のものが実際よりも近く見えたり大きく見えたりすることで体験できます.この様に,異なる材質(例えば,空気から水に)に向かって光が進入するときに,光の進む方向が曲がることを「光の屈折」と呼びます.
ではどうして,光は屈折するのでしょうか.それは,材質の中を光が通過するときにその通過する速度が違うためなのです.感覚的に考えれば,私たちが水の中を歩くのと,陸上を歩くのとでは,陸上の方がずっと速く歩ける事で理解できるでしょう.空気より水の方が密度が高いから,その分抵抗が大きくなる,だから速く歩けない.大ざっぱにいえば,光も同じように考えていいでしょう.「光は,密度の高い材質を通過するときには,通過速度がその分だけ遅くなります.」
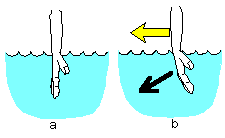
下の図aのように,手首までを水に浸けてみます.それから,bの様に黄色の矢印の方に手を動かすと,手は水の抵抗のため自然に曲がりますね.その時,手の甲はやや下を向くでしょう.実は,光の進行方向を,この手の方向で表わすことができます.手の甲の向きのことを光の場合には,「波面」と呼びます.つまり,屈折率が高いところに光が進入すると,その抵抗のために光の波面は曲げられて,その結果光の進行方向が曲がるのです.これが光の屈折です.
屈折の度合いは,物質によって様々で,それぞれ特有(固有)の値を持ちます.
- 複屈折
ある種の物質では,境界面で屈折する光がひとつではなく,2つになるものがあります.この様な物質に光を入射させると,光は2つの方向に屈折します.この物質を通してものを見ると向こう側が二重に見えて結構面白いですよ.
この様な現象を「複屈折」と呼びます.なぜなら,<屈折>する方向が<複>数あるから.これをもう少し物理的に考えてみましょう.
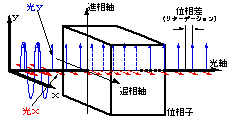
複屈折は,物質中を光が通過するとき,振動面の向きによってその進む速度が異なることをいいます.この様子を図に示します.図では,X方向に振動する光がY方向のそれよりも試料の中をゆっくり通過しています.その結果,試料から出た光は,通過速度の差の分だけ「位相差」が生じることになります.これは,X軸とY軸とで光学的に違う性質(光の通過速度=屈折率が異なる)を持つからです.光学では,物質内を透過するときの光の速度Vと,真空中での光の速度cとの比[n=c/V]を「屈折率」と呼びます.ですから,光の振動面の向きによって屈折率が異なることから「複屈折」というわけです.
光の進む速度が速い(位相が進む)方位をその位相子の「進相軸」,反対に遅い(位相が遅れる)方位を「遅相軸」と呼びます.進相軸と遅相軸とを総称して,複屈折の「主軸」という呼び方もします.
たとえば,試料Aと試料Bにそれぞれ光を透過させたとき,試料Aの方が大きな位相差を示したとすると,「試料Aは試料Bよりも複屈折が大きい.」といいます.また,複屈折のある試料は「光学的に異方性」があるといい,ガラスなどのように普通の状態では複屈折を示さない試料を「等方性試料」といいます.
高分子配向膜,液晶高分子,光学結晶,などは,複屈折性を示します.また,等方性の物質でも外部から応力を加えたりすると一時的に異方性を示し(光弾性効果),複屈折を生じます.
以上のように複屈折の大きさは,位相差として検出・定量化することが出来ます.この時の単位は,一般に波の位相を角度で表した値が使われます.たとえば,1波長の位相差があるときには「位相差=360度(deg.)」となります.同じように考えて,二分の一波長板の位相差は180度,四分の一波長板は90度となります.
しかし,角度を用いた表現では,360度に対応する波長の長さが限定できないと絶対的な大きさは表せないことになります.角度の表示は,1波長=360度が基準になっているからです.このため,測定光の波長が,He-Neレーザーの633 nmの時と,1520 nmの時とでは,「位相差=10度」と同じ値を示しても,絶対量は違うことになってしまいます.
この様な紛らわしさを防ぐために,位相差を波長で規格化して,長さの単位に換算して表すこともあります.この時の単位は普通,「nm(ナノメーター)」が用いられます.例えば,波長633 nmで測定したときの位相差が15度だったときの複屈折量は,
15 x 633 / 360 = 26.4 (nm)
となります.このように,複屈折量の大きさを,便宜上,位相差の大きさで表すことが一般的になっています.
複屈折量を表すときには,同時に複屈折主軸の方位も重要な要素となります.逆に言えば,複屈折量を測定したいときには,その試料の複屈折主軸の方位を知らないと大きさを規定できない,といえます.複屈折主軸の方位を表すときの単位は,角度(deg.)を用いるのが普通です.方位は,その測定器の持つ方位軸(例えば,定盤に平行な方位を0度とする,というように分かりやすい方位を決める)を基準にするのが一般的です.
Back Next


