What birefringence is
- Refraction of Light
When light enters a transparent material from the air, it bends at the boundary. In other words, the direction of travel changes. The reason for this is that the properties of air and transparent materials are different. In our daily life, when we take a bath or go into a pool, our arms appear to bend at the surface of the water, and objects in the water appear closer or larger than they actually are. In this way, when light enters a different material (for example, from air to water), the direction in which the light travels is bent, which is called “refraction of light.
So why does light refract? It is because the speed at which light passes through a material is different from the speed at which it passes through the material. If we think about it from a sensory point of view, we can understand that we can walk much faster on land than we can in water. Because water is denser than air, the resistance is greater, and so we cannot walk as fast. Roughly speaking, you can think of light in the same way. When light passes through a denser material, it passes slower by that amount.
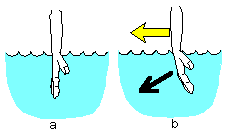
Immerse your wrist in water, as shown in figure a below. Then, move your hand toward the yellow arrow as shown in b. Your hand will bend naturally due to the resistance of the water. At that time, the back of your hand will point slightly downward. In fact, the direction of the light can be expressed by the direction of the hand. The direction of the back of the hand is called the “wavefront” in the case of light. In other words, when light enters a place with a high refractive index, the wavefront of the light is bent due to its resistance, and as a result, the direction of light travel is bent. This is the refraction of light.
The degree of refraction varies from material to material, and each has its own specific (intrinsic) value.
- Birefringence
In some materials, the light refracted at the boundary surface is not one, but two. When light is incident on such a material, it is refracted in two directions. When you look at something through this material, you can see the other side twice, which is quite interesting.
This phenomenon is called “birefringence”. This phenomenon is called “birefringence” because there are “multiple” directions of refraction. Let’s think about this in more physical terms.
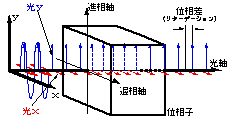
Birefringence refers to the fact that when light passes through a material, the speed at which it travels differs depending on the direction of the vibrating surface. The figure below shows this phenomenon. In the figure, the light oscillating in the X direction passes through the sample more slowly than that in the Y direction. As a result, the light emitted from the sample has a “phase difference” due to the difference in speed of passage. This is because the x-axis and the y-axis have different optical properties (different light transit speed = different refractive index). In optics, the refractive index is the ratio [n=c/V] of the speed of light in a vacuum to the speed V of light as it passes through a material. Therefore, the term “birefringence” refers to the fact that the refractive index differs depending on the direction of the vibrating surface of the light.
The direction in which light travels faster (in phase) is called the “phase advance axis” of the phasor, and the direction in which light travels slower (out of phase) is called the “phase retardation axis. The phase advance axis and the phase retardation axis are collectively called the “principal axes” of birefringence.
For example, when light is transmitted through sample A and sample B, and sample A shows a larger phase difference than sample B, it is said that “sample A has a larger birefringence than sample B. Sample A has greater birefringence than sample B. A sample with birefringence is said to be “optically anisotropic,” while a sample that does not show birefringence in its normal state, such as glass, is called an “isotropic sample.
Oriented polymer films, liquid crystal polymers, optical crystals, etc. exhibit birefringence. Even isotropic materials temporarily show anisotropy (photoelastic effect) when stress is applied externally, resulting in birefringence.
As described above, the magnitude of birefringence can be detected and quantified as phase difference. The unit of measurement is generally the value of the phase of the wave expressed as an angle. For example, if there is a phase difference of one wavelength, the unit is “phase difference = 360 degrees (deg.). In the same way, the phase difference of a half-wave plate is 180 degrees, and that of a quarter-wave plate is 90 degrees.
However, the absolute magnitude cannot be expressed using an angle unless the length of the wavelength corresponding to 360 degrees can be limited. This is because the indication of angle is based on one wavelength = 360 degrees. Therefore, if the wavelength of the measurement light is 633 nm or 1520 nm of He-Ne laser, the absolute amount will be different even if the same value of “phase difference = 10 degrees” is shown.
In order to avoid such confusion, the phase difference is sometimes standardized by wavelength and converted to a unit of length. In this case, “nm (nanometer)” is usually used as the unit. For example, if the phase difference is 15 degrees when measured at a wavelength of 633 nm, the amount of birefringence is
15 x 633 / 360 = 26.4 (nm)
For example, if the phase difference is 15 degrees when measured at 633 nm, the birefringence is 15 x 633 / 360 = 26.4 (nm). Thus, it is common to express the magnitude of birefringence as the magnitude of the phase difference for convenience.
When expressing the amount of birefringence, the orientation of the principal axis of birefringence is also an important factor. The orientation of the birefringent principal axis is also an important factor when expressing birefringence. The unit used to express the orientation of the birefringent principal axis is usually angle (deg.). The azimuth is usually based on the azimuth axis of the instrument (for example, the azimuth parallel to the surface plate is 0 degrees).
Back Next


